사실 Matlab을 할 줄 알아도 어디에 사용해야 할지 모르는 사람이 아주 많습니다. 그리고 수식을 알더라도 이것을 Matlab으로 코드화하는 방법을 어려워하시는 분들이 많습니다. 이번 포스팅에서는 간단한 3차원 수식을 활용하여 3D 형상을 만들어보는 예제를 진행해 보도록 하겠습니다.
3차원 관련 수식
- 평면에서의 Ellipsoid (타원)

위 수식에서 타원의 중심은 (Xo, Yo, Zo)이며 a, b, c는 x, y, z 축의 센터에서 부터의 길이를 의미합니다.

위 수식에서 저희는 Z를 중심으로 수식을 변경할 것이며 X, Y 평면에 그려 나갈 것입니다. X, Y일 때 높이 값을 Z로 구하는 것이죠.

자 이제 모든 것은 끝이 났습니다. X, Y의 범위만 제가 정해주고 코드를 구성해 주면 Xn, Yn일 때의 Zn이 나오겠죠?
이제 X축의 범위를 정하고, Y축의 범위를 정해서 넣어주면 Z 값이 나오게 됩니다.

3차원 관련 예제
위의 수식을 활용하여 다양한 3차원 수식을 코드화하여 나타내면 아래와 같습니다.




뭔가 이상한 점이 있지 않나요? 왜 아래쪽은 없지? 제가 하는 일에서는 아래쪽은 그다지 필요하지 않습니다. 물론 조금만 수정하면 여러분이 다 표현할 수 있도록 코드를 작성하였습니다. 위의 3차원 도형을 활용하여 저는 아래와 같이 사용합니다.


위처럼 인공 해저 지형을 모사하기도 하고 아래처럼 사람이나 자전거의 이미지를 따서 데이터화해서 같이 접목시켜 특수한 환경의 해상 조건을 만들어서 시뮬레이션을 하기도 합니다.
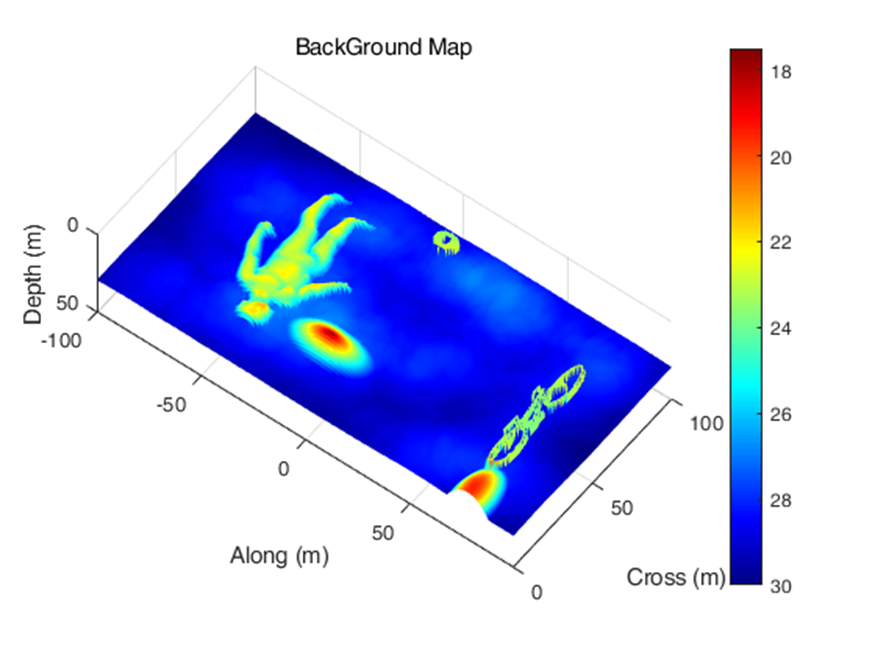
글 쓰다 보니 너무 멀리 온 것 같네요. 결론은 3차원 도형이라 함은 3개의 변수(x, y, z)를 가진 수식으로 이루어져 있습니다.
그중 하나의 축을 기준으로 정렬을 하시고 x, y의 범위를 정해주시면 자연스럽게 z 축에 대한 결과 값을 볼 수 있습니다. 이런 식으로 응용하여 다양한 수식을 시각화하시길 바랍니다.
아 물론 단순 타원을 원하시면
ellipsoid(0,-0.5,0,6,3.25,3.25)위 함수를 사용하시면 됩니다. 근데 이렇게 되면 다른 도형은 어떻게 활용을 하나요.. 편리한 건 있지만 딱 거기서 끝입니다. 하나씩 하나씩 연습해 보시길 바랍니다.

3차원 도형 코드 다운로드
'Matlab' 카테고리의 다른 글
| 초보자가 Jetson Nano(미니피시) 간단하게 Matlab과 연결 하기 (1) | 2024.04.01 |
|---|---|
| Matlab resample과 upsample, downsample 차이점 (0) | 2023.06.28 |
| Matlab FFT 엄청 쉽게 활용하는 방법 (0) | 2023.06.01 |
| Matlab 행렬 길이가 다른 데이터 하나로 처리하기(CELL) (0) | 2023.05.29 |
| Matlab 논문 쓸 때 필수 그래프 오차 막대 그리기(코드 첨부) (0) | 2023.05.29 |



댓글